Category theory notes

notes

Does rhyming form a category with a set of random words and a rhyming operator? ##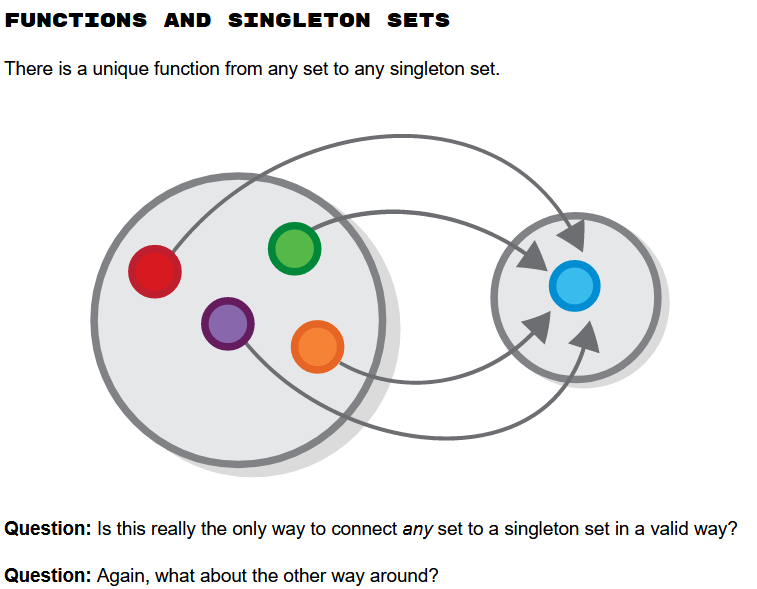

Is this really the case?

Groups

If we view monoids as a means of modeling the effect of applying a set of (associative) actions, we use groups to model the effects of actions (that) are also reversible.

All cyclic groups that have the same number of elements (or that are of the same order) are isomorphic to each other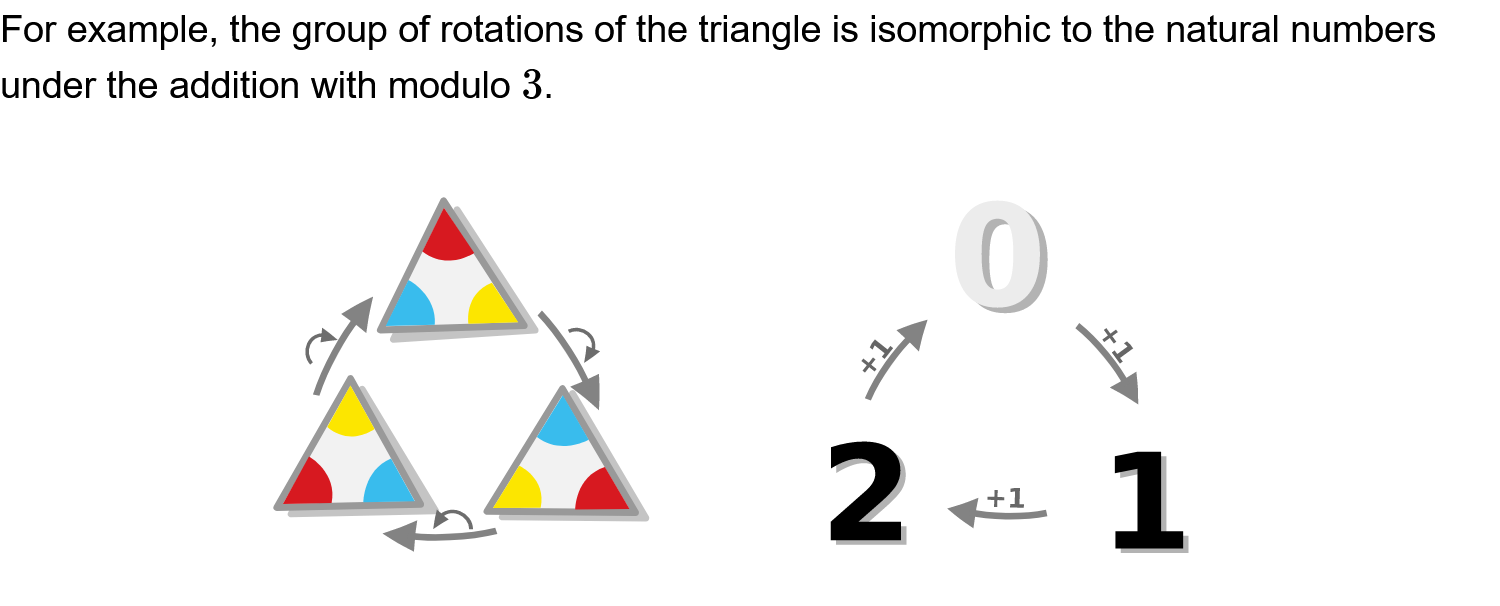

Journal

6/29/2024

I need to have chat GB Teach me logic but do it through English so I can incorporate it with rapping and internalize it. so I can know it innately. so I can become the math. so I can become the myth. so I can become the math!!!

if my hair is brown, then my hair is also either blond or brown. This is what or means, right?

From this viewpoint, the function can be viewed as instance of a logical rule of inference called conjunction elimination (also called simplification) stating that, , for example, if your hair is partly blond and partly brown, then it is partly blond.

I want to know if I can create some kind of chainReaction with logic and categoriess Such that it’s an infinite loop that does self discovery over concepts and combines those to try and reach other new ones and validate whether or not they’re true and continues to combine those and accumulate them a search over truth?

You can represent sentences as an ordered tuple of words

An automatic graph searching for composable combinations of categories in both directions you don’t know where you are in the actual chain IE you can’t assume you’ve started at the simplest category.

Products as Objects

IMPORTANT

In the previous chapter, we established the correspondence of various concepts in programming languages and set theory — sets resemble types, functions resemble methods/subroutines. This picture is made complete with products, that are like stripped-down classes (also called records or structs) — the sets that form the product correspond to the class’s properties (also called members) and the functions for accessing them are like what programmers call getter methods e.g. the famous example of object-oriented programming of a Person class with name and age fields is nothing more than a product of the set of strings, and the sets of numbers. And objects with more than two values can be expressed as products the composites of which are themselves products.

Is category theory the algebra of relationships?

Because a set is defined only by the items it contains, the empty set is unique — there is no difference between the set that contains zero balls and the set that contains zero numbers, for instance.

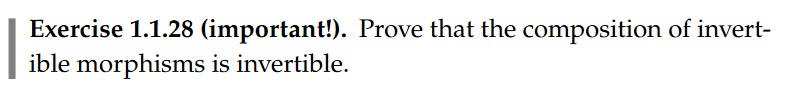
ME:

I think that Given a category C that is associative and commutative, as long as any Homomorphisms that are done that preserve the structure of C composition will be preserved. Composition as an operation on homomorphisms that does not change the structure of the category and therefore An invertible function that’s composed with another invertible function will self be invertible.

CGPT

It seems like you’re trying to articulate a proof about the composition of invertible morphisms in a category. However, the statement is a bit unclear and could benefit from some refinement for clarity and correctness. Here’s a revised version based on my understanding:

Revised Statement:

In a category ( ), if ( f: A B ) and ( g: B A ) are invertible morphisms (i.e., there exist morphisms ( f^{-1}: B A ) and ( g^{-1}: A B ) such that ( f f^{-1} = _B ), ( f^{-1} f = _A ), ( g g^{-1} = _A ), and ( g^{-1} g = _B )), then the composition ( g f: A A ) is also invertible, with inverse ( f^{-1} g^{-1}: A A ).

Explanation:

• In a category where morphisms behave associatively and composition respects identities (associative and unital properties), if ( f ) and ( g ) are invertible, their composition ( g f ) remains invertible.
• This follows because the existence of inverses ensures that ( (g f) (f^{-1} g^{-1}) = _A ) and ( (f^{-1} g^{-1}) (g f) = _A ), demonstrating that ( g f ) has an inverse ( f^{-1} g^{-1} ).

If this matches your intended proof, it’s a fundamental property of categories and morphisms. Let me know if you have further questions or if there’s a specific aspect you’d like to explore!

Sure! Let’s start with a crash course on groups.

Definition of a Group

A group is a set ( G ) combined with an operation ( ) (often called multiplication) that satisfies four main properties:

1. Closure: For all ( a, b G ), the result of the operation ( a b ) is also in ( G ).
2. Associativity: For all ( a, b, c G ), ( (a b) c = a (b c) ).
3. Identity Element: There exists an element ( e G ) such that for every ( a G ), ( e a = a e = a ). This element ( e ) is called the identity element.
4. Inverse Element: For each ( a G ), there exists an element ( b G ) such that ( a b = b a = e ), where ( e ) is the identity element. The element ( b ) is called the inverse of ( a ).

Example of a Group

A classic example of a group is the set of integers ( ) with the operation of addition ( + ).

1. Closure: If ( a ) and ( b ) are integers, then ( a + b ) is also an integer.
2. Associativity: For all integers ( a, b, c ), ( (a + b) + c = a + (b + c) ).
3. Identity Element: The identity element is ( 0 ) because ( a + 0 = 0 + a = a ) for any integer ( a ).
4. Inverse Element: For each integer ( a ), the inverse is ( -a ) because ( a + (-a) = (-a) + a = 0 ).

Simple Example Problems

1. Problem 1: Show that the set of integers ( ) with addition forms a group.

   Solution:

   • Closure: If ( a, b ), then ( a + b ).
   • Associativity: For all ( a, b, c ), ( (a + b) + c = a + (b + c) ).
   • Identity Element: ( 0 ) is the identity element because ( a + 0 = a ) for any ( a ).
   • Inverse Element: For each ( a ), the inverse is ( -a ) because ( a + (-a) = 0 ).

2. Problem 2: Determine if the set of positive integers ( ^+ ) with multiplication forms a group.

   Solution:

   • Closure: If ( a, b ^+ ), then ( a b ^+ ).
   • Associativity: For all ( a, b, c ^+ ), ( (a b) c = a (b c) ).
   • Identity Element: The identity element is ( 1 ) because ( a = 1 a = a ) for any ( a ^+ ).
   • Inverse Element: This is where it fails. Not every positive integer has an inverse in ( ^+ ). For example, there is no positive integer ( b ) such that ( 2 b = 1 ). Hence, ( ^+ ) with multiplication is not a group.

Proof Example

Let’s prove that the set of non-zero rational numbers ( ^* ) with multiplication forms a group.

1. Closure: If ( a, b ^* ), then ( a b ^* ). Since both ( a ) and ( b ) are non-zero rational numbers, their product is also a non-zero rational number.

2. Associativity: For all ( a, b, c ^* ), ( (a b) c = a (b c) ). This follows from the associativity of multiplication in the real numbers.

3. Identity Element: The identity element is ( 1 ) because ( a = 1 a = a ) for any ( a ^* ).

4. Inverse Element: For each ( a ^* ), the inverse is ( ) because ( a = a = 1 ).

Since ( ^* ) with multiplication satisfies all four properties, it is a group.

I hope this helps! If you have any specific questions or need further clarification, feel free to ask.

me

So what the book was kind of trying to tell me is that I can kind of look at a category as a group with a set of operations that only require closure and associativity to be a category is that correct?

Definition

The definition of a Category From starting set theory by Paolo Perrone p1:

Definition

Consider A collection w; ### 2.Binary operation: Consider the function ℜ(w)->w EX: (dog)->log

What’s interesting to me here is that the heuristic for how w is obtained doesn’t matter. all that matters or all that we need to know is that ℜ of w returns w. ### 3. The operation is associative:

graph LR
                dog("A: dog") -->|F| log("B: log")
                log -->|G| cog("C: cog")
                dog -->|H| cog

4. The set contains the neutral element.

In this case the neutral element can be many words depending on the context. Bit like music in that way as in when you’re descending things are different versus when you’re ascending even if you’re using the same notes. Consider this example:

Definition of a perfect rhyme: A rhyme in which every syllable in word a rhymes with every syllable in word b.

Assume that all words that perfectly rhyme are the neutral element. IE:

ℜ(a)->b ℜ(dog)->log

It’s almost a bit like congruency. Like I should see how to form a category out of that and maybe it could help me. But for right now it feels right that two perfect rhymes should give another perfect rhyme which is a neutral element.

5. The set is closed under the operation

By definition the rhyming function ℜ(w)->w is closed under the operation. ## Exercises ### 1.1.34 I’m not gonna do it right now but I think this one is really important so I can automatically at a glance graphically know what type of morphisms I’m looking at. Idealistically this needs to be well known.